what is the solubility of cr(oh)3 when added to a ph 13 solution

17.4 Solubility and pH

Learning Objective

1. To sympathize why the solubility of many compounds depends on pH.

The solubility of many compounds depends strongly on the pH of the solution. For example, the anion in many sparingly soluble salts is the conjugate base of a weak acid that may get protonated in solution. In addition, the solubility of elementary binary compounds such as oxides and sulfides, both strong bases, is frequently dependent on pH. In this section, we hash out the relationship betwixt the solubility of these classes of compounds and pH.

The Consequence of Acid–Base of operations Equilibriums on the Solubility of Salts

We begin our discussion past examining the event of pH on the solubility of a representative common salt, Thou⁺A⁻, where A⁻ is the conjugate base of the weak acid HA. When the salt dissolves in water, the post-obit reaction occurs:

Equation 17.thirteen

$$\begin{array}{cc}\hfill \text{MA(s)}\rightleftharpoons {\text{M}}^{+}\text{(aq)}+{\text{A}}^{-}\text{(aq)}& {\mathrm{Thou}}_{\text{sp}}=[{\text{1000}}^{+}][{\text{A}}^{-}]\end{array}$$

The anion can also react with water in a hydrolysis reaction:

Equation 17.14

$${\text{A}}^{-}\text{(aq)}+{\text{H}}_{\mathrm{ii}}\text{O(fifty)}\rightleftharpoons {\text{OH}}^{-}\text{(aq)}+\text{HA(aq)}$$

Because of the reaction described in Equation 17.fourteen, the predicted solubility of a sparingly soluble common salt that has a basic anion such as S²⁻, PO_four ³⁻, or CO_three ²⁻ is increased, as described in Section 17.1 "Determining the Solubility of Ionic Compounds". If instead a stiff acid is added to the solution, the added H⁺ volition react essentially completely with A⁻ to form HA. This reaction decreases [A⁻], which decreases the magnitude of the ion product (Q = [Grand⁺][A⁻]). Co-ordinate to Le Châtelier's principle, more MA will dissolve until Q = K _sp. Hence an acidic pH dramatically increases the solubility of virtually all sparingly soluble salts whose anion is the cohabit base of operations of a weak acid. In contrast, pH has piddling to no issue on the solubility of salts whose anion is the conjugate base of operations of a stronger weak acrid or a strong acid, respectively (e.one thousand., chlorides, bromides, iodides, and sulfates). For instance, the hydroxide salt Mg(OH)_two is relatively insoluble in water:

Equation 17.15

$$\begin{array}{cc}\hfill {\text{Mg(OH)}}_{\mathrm{ii}}\text{(s)}\rightleftharpoons {\text{Mg}}^{2+}\text{(aq)}+2{\text{OH}}^{-}\text{(aq)}& K_{\text{sp}}=5.61\times {10}^{-12}\end{array}$$

When acid is added to a saturated solution that contains excess solid Mg(OH)_ii, the following reaction occurs, removing OH⁻ from solution:

Equation 17.xvi

$${\text{H}}^{+}\text{(aq)}+{\text{OH}}^{-}\text{(aq)}\to {\text{H}}_2\text{O(l)}$$

The overall equation for the reaction of Mg(OH)₂ with acrid is thus

Equation 17.17

$${\text{Mg(OH)}}_{\text{2}}\text{(south)}+{\text{2H}}^{+}\text{(aq)}\rightleftharpoons {\text{Mg}}^{\text{two+}}\text{(aq)}+{\text{2H}}_{\text{2}}\text{O(l)}$$

As more acid is added to a suspension of Mg(OH)₂, the equilibrium shown in Equation 17.17 is driven to the right, so more Mg(OH)₂ dissolves.

Such pH-dependent solubility is non restricted to salts that contain anions derived from h2o. For instance, CaF_two is a sparingly soluble salt:

Equation 17.eighteen

$$\begin{array}{cc}\hfill {\text{CaF}}_2\text{(s)}\rightleftharpoons {\text{Ca}}^{\mathrm{two}+}\text{(aq)}+2{\text{F}}^{-}\text{(aq)}& K_{\text{sp}}=3.45\times {10}^{-11}\end{array}$$

When strong acid is added to a saturated solution of CaF₂, the following reaction occurs:

Equation 17.19

$${\text{H}}^{+}\text{(aq)}+{\text{F}}^{-}\text{(aq)}\rightleftharpoons \text{HF(aq)}$$

Because the forward reaction decreases the fluoride ion concentration, more CaF_two dissolves to relieve the stress on the system. The net reaction of CaF₂ with strong acid is thus

Equation 17.20

CaF_two(s) + 2H⁺(aq) → Ca²⁺(aq) + 2HF(aq)

Example seven shows how to summate the solubility effect of calculation a stiff acid to a solution of a sparingly soluble salt.

Note the Pattern

Sparingly soluble salts derived from weak acids tend to exist more soluble in an acidic solution.

Case seven

Pb oxalate (PbC_iiO₄), lead iodide (PbI₂), and lead sulfate (PbSO₄) are all rather insoluble, with K _sp values of 4.8 × x⁻¹⁰, 9.8 × 10⁻⁹, and 2.53 × 10⁻⁸, respectively. What effect does adding a strong acid, such as perchloric acrid, accept on their relative solubilities?

Given: K _sp values for iii compounds

Asked for: relative solubilities in acid solution

Strategy:

Write the balanced chemical equation for the dissolution of each salt. Because the strongest conjugate base will be virtually affected by the add-on of potent acrid, decide the relative solubilities from the relative basicity of the anions.

Solution:

The solubility equilibriums for the iii salts are equally follows:

$$\begin{array}{c}\hfill {\text{PbC}}_2{\text{O}}_{\mathrm{four}}\text{(southward)}\rightleftharpoons {\text{Pb}}^{2+}\text{(aq)}+{\text{C}}_2{\text{O}}_4{}^{2-}\text{(aq)}\\ \hfill {\text{PbI}}_2\text{(s)}\rightleftharpoons {\text{Pb}}^{2+}\text{(aq)}+\mathrm{two}{\text{I}}^{-}\text{(aq)}\\ \hfill {\text{PbSO}}_{\mathrm{iv}}\text{(south)}\rightleftharpoons {\text{Pb}}^{2+}\text{(aq)}+{\text{And then}}_4{}^{2-}\text{(aq)}\end{array}$$

The addition of a strong acid will have the greatest event on the solubility of a common salt that contains the conjugate base of a weak acrid equally the anion. Because HI is a potent acid, we predict that adding a stiff acid to a saturated solution of PbI_two will non greatly affect its solubility; the acid will simply dissociate to grade H⁺(aq) and the corresponding anion. In dissimilarity, oxalate is the fully deprotonated class of oxalic acrid (HO_iiCCO_iiH), which is a weak diprotic acid (p1000 _a1 = 1.23 and pThou _a2 = 4.xix). Consequently, the oxalate ion has a meaning affinity for ane proton and a lower affinity for a 2d proton. Calculation a strong acid to a saturated solution of lead oxalate will result in the following reactions:

$$\begin{array}{c}\hfill {\text{C}}_2{\text{O}}_4{}^{2-}\text{(aq)}+{\text{H}}^{+}\text{(aq)}\to {\text{HO}}_{\mathrm{ii}}{\text{CCO}}_2{}^{-}\text{(aq)}\\ \hfill {\text{HO}}_{\mathrm{ii}}{\text{CCO}}_2{}^{-}\text{(aq)}+{\text{H}}^{+}\text{(aq)}\to {\text{HO}}_2{\text{CCO}}_{\mathrm{two}}\text{H(aq)}\end{array}$$

These reactions will decrease [C₂O_four ²⁻], causing more lead oxalate to dissolve to relieve the stress on the organisation.The pK _a of HSO₄ ⁻ (1.99) is similar in magnitude to the pYard _a1 of oxalic acid, then adding a strong acrid to a saturated solution of PbSO₄ volition result in the following reaction:

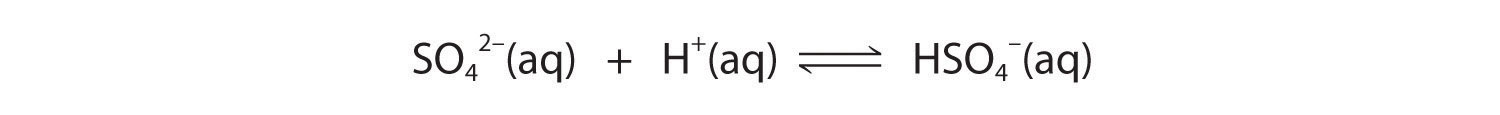
Because HSO₄ ⁻ has a pKa of 1.99, this reaction will lie largely to the left every bit written. Consequently, we predict that the consequence of added strong acrid on the solubility of PbSO₄ will be significantly less than for PbC_iiO_iv.

Exercise

Which of the following insoluble salts—AgCl, Ag₂CO_iii, Ag_iiiPO_iv, and/or AgBr—will exist substantially more soluble in 1.0 M HNO₃ than in pure water?

Reply: Ag₂CO₃ and Ag_iiiPO₄

Caves and their associated pinnacles and spires of stone provide one of the nigh impressive examples of pH-dependent solubility equilibriums (office (a) in Figure 17.6 "The Chemistry of Cave Formation"). Perhaps the most familiar caves are formed from limestone, such as Carlsbad Caverns in New Mexico, Mammoth Cave in Kentucky, and Luray Caverns in Virginia. The master reactions that are responsible for the formation of limestone caves are as follows:

Equation 17.21

$${\text{CO}}_2\text{(aq)}+{\text{H}}_{\mathrm{two}}\text{O(fifty)}\rightleftharpoons {\text{H}}^{+}{\text{(aq) + HCO}}_3{}^{-}\text{(aq)}$$

Equation 17.22

$${\text{HCO}}_3{}^{-}\text{(aq)}\rightleftharpoons {\text{H}}^{+}\text{(aq)}+{\text{CO}}_{\mathrm{iii}}{}^{2-}\text{(aq)}$$

Equation 17.23

$${\text{Ca}}^{2+}\text{(aq)}+{\text{CO}}_3{}^{2-}\text{(aq)}\rightleftharpoons {\text{CaCO}}_3\text{(s)}$$

Figure 17.6 The Chemistry of Cavern Formation

(a) This cave in Campanet, Mallorca, Spain, and its associated formations are examples of pH-dependent solubility equilibriums. (b) A cave forms when groundwater containing atmospheric CO_ii, forming an acidic solution, dissolves limestone (CaCO₃) in a procedure that may take tens of thousands of years. As groundwater seeps into a cavern, water evaporates from the solution of CaCO_three in CO_two-rich water, producing a supersaturated solution and a shift in equilibrium that causes precipitation of the CaCO₃. The deposited limestone eventually forms stalactites and stalagmites.

Limestone deposits that form caves consist primarily of CaCO₃ from the remains of living creatures such as clams and corals, which used it for making structures such as shells. When a saturated solution of CaCO₃ in CO_ii-rich water rises toward Earth's surface or is otherwise heated, CO₂ gas is released as the h2o warms. CaCO₃ then precipitates from the solution according to the following equation (part (b) in Figure 17.half-dozen "The Chemistry of Cave Germination"):

Equation 17.24

$${\text{Ca}}^{2+}\text{(aq)}+\mathrm{two}{\text{HCO}}_{\mathrm{three}}{}^{-}\text{(aq)}\rightleftharpoons {\text{CaCO}}_3\text{(s)}+{\text{CO}}_2\text{(g)}+{\text{H}}_2\text{O(50)}$$

The forward direction is the same reaction that produces the solid called scale in teapots, coffee makers, h2o heaters, boilers, and other places where hard h2o is repeatedly heated.

When groundwater-containing atmospheric CO₂ (Equation 17.21 and Equation 17.22) finds its way into microscopic cracks in the limestone deposits, CaCO_three dissolves in the acidic solution in the reverse direction of Equation 17.24. The cracks gradually enlarge from 10–50 µm to 5–10 mm, a process that can take equally long as ten,000 yr. Eventually, after about some other 10,000 twelvemonth, a cave forms. Groundwater from the surface seeps into the cave and clings to the ceiling, where the h2o evaporates and causes the equilibrium in Equation 17.24 to shift to the right. A circular layer of solid CaCO₃ is deposited, which somewhen produces a long, hollow spire of limestone called a stalactite that grows down from the ceiling. Below, where the droplets country when they fall from the ceiling, a similar procedure causes another spire, called a stalagmite, to grow upwards. The same processes that carve out hollows beneath ground are also at work to a higher place ground, in some cases producing fantastically convoluted landscapes like that of Yunnan Province in China (Figure 17.seven "Solubility Equilibriums in the Germination of Karst Landscapes").

Effigy 17.7 Solubility Equilibriums in the Formation of Karst Landscapes

Landscapes such equally the steep limestone pinnacles of the Stone Forest in Yunnan Province, China, are formed from the same procedure that produces caves and their associated formations.

Acidic, Basic, and Amphoteric Oxides and Hydroxides

One of the earliest classifications of substances was based on their solubility in acidic versus basic solution, which led to the nomenclature of oxides and hydroxides every bit being either basic or acidic. Basic oxidesAn oxide that reacts with water to produce a bones solution or dissolves readily in aqueous acid. and hydroxides either react with water to produce a basic solution or deliquesce readily in aqueous acid. Acidic oxidesAn oxide that reacts with h2o to produce an acidic solution or dissolves in aqueous base. or hydroxides either react with water to produce an acidic solution or are soluble in aqueous base. Every bit shown in Effigy 17.eight "Nomenclature of the Oxides of the Main Grouping Elements According to Their Acidic or Basic Character", there is a articulate correlation betwixt the acidic or the bones character of an oxide and the position of the element combined with oxygen in the periodic tabular array. Oxides of metallic elements are generally basic oxides, and oxides of nonmetallic elements are acidic oxides. Compare, for example, the reactions of a typical metallic oxide, cesium oxide, and a typical nonmetal oxide, sulfur trioxide, with h2o:

Equation 17.25

$${\text{Cs}}_2\text{O(s)}+{\text{H}}_{\mathrm{two}}\text{O(l)}\to {\text{2Cs}}^{+}\text{(aq)}+2{\text{OH}}^{-}\text{(aq)}$$

Equation 17.26

$${\text{SO}}_3\text{(g)}+{\text{H}}_{\mathrm{ii}}\text{O(50)}\to {\text{H}}_2{\text{Then}}_4\text{(aq)}$$

Cesium oxide reacts with water to produce a basic solution of cesium hydroxide, whereas sulfur trioxide reacts with h2o to produce a solution of sulfuric acrid—very different behaviors indeed!

Notation the Blueprint

Metal oxides more often than not react with h2o to produce bones solutions, whereas nonmetal oxides produce acidic solutions.

The departure in reactivity is due to the difference in bonding in the 2 kinds of oxides. Because of the depression electronegativity of the metals at the far left in the periodic tabular array, their oxides are best viewed as containing discrete 1000due north ⁺ cations and O²⁻ anions. At the other end of the spectrum are nonmetal oxides; due to their higher electronegativities, nonmetals form oxides with covalent bonds to oxygen. Because of the high electronegativity of oxygen, however, the covalent bond between oxygen and the other cantlet, E, is normally polarized: E^δ+–O^δ−. The atom E in these oxides acts as a Lewis acid that reacts with the oxygen atom of water to produce an oxoacid. Oxides of metals in high oxidation states also tend to exist acidic oxides for the same reason: they incorporate covalent bonds to oxygen. An instance of an acidic metallic oxide is MoO₃, which is insoluble in both water and acid but dissolves in strong base of operations to give solutions of the molybdate ion (MoO₄ ²⁻):

Equation 17.27

MoO₃(s) + 2OH⁻(aq) → MoO₄ ²⁻(aq) + H₂O(l)

As shown in Figure 17.8 "Classification of the Oxides of the Chief Grouping Elements According to Their Acidic or Basic Character", there is a gradual transition from bones metal oxides to acidic nonmetal oxides as nosotros go from the lower left to the upper right in the periodic tabular array, with a wide diagonal band of oxides of intermediate character separating the two extremes. Many of the oxides of the elements in this diagonal region of the periodic tabular array are soluble in both acidic and bones solutions; consequently, they are called amphoteric oxidesAn oxide that tin dissolve in acrid to produce water and dissolve in base to produce a soluble complex. (from the Greek ampho, significant "both," equally in amphiprotic, which was divers in Chapter 16 "Aqueous Acid–Base of operations Equilibriums", Section sixteen.i "The Autoionization of H2o"). Amphoteric oxides either dissolve in acid to produce water or dissolve in base to produce a soluble complex. As shown in Figure 17.9 "Chromium(III) Hydroxide [Cr(OH)", for example, mixing the amphoteric oxide Cr(OH)₃ (also written as Cr₂O₃·3H₂O) with water gives a muddied, purple-brown intermission. Adding acid causes the Cr(OH)_three to dissolve to give a bright violet solution of Crⁱⁱⁱ⁺(aq), which contains the [Cr(H₂O)₆]³⁺ ion, whereas calculation strong base of operations gives a dark-green solution of the [Cr(OH)₄]⁻ ion. The chemic equations for the reactions are as follows:

Equation 17.28

$${\text{Cr(OH)}}_3\text{(s)}+3{\text{H}}^{+}\text{(aq)}\to \underset{\text{violet}}{{\text{Cr}}^{\mathrm{three}+}\text{(aq)}}+\mathrm{three}{\text{H}}_2\text{O(l)}$$

Equation 17.29

$${\text{Cr(OH)}}_3\text{(s)}+{\text{OH}}^{-}\text{(aq)}\to \underset{\text{light-green}}{{[{\text{Cr(OH)}}_4]}^{-}}\text{(aq)}$$

Figure 17.viii Classification of the Oxides of the Chief Group Elements According to Their Acidic or Basic Character

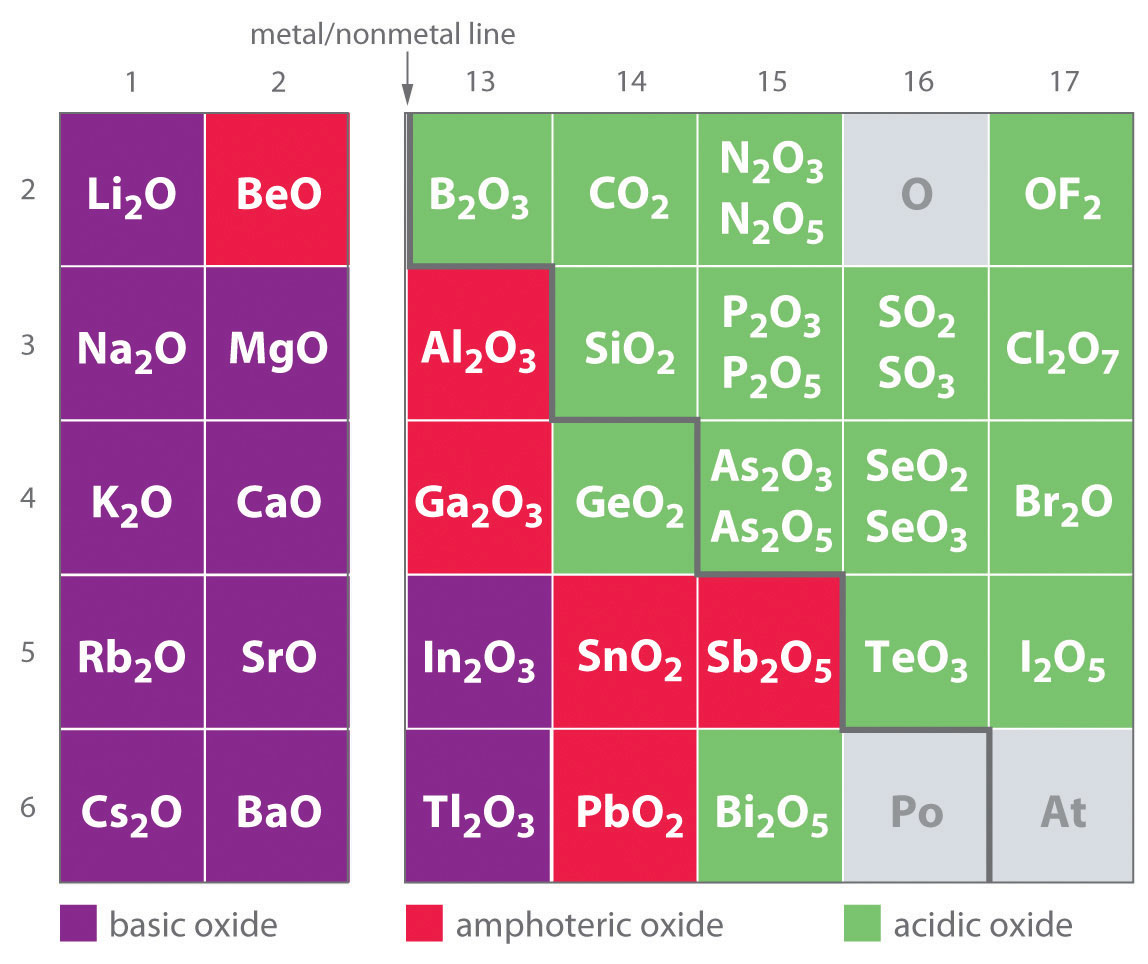
There is a gradual transition from bones oxides to acidic oxides from the lower left to the upper correct in the periodic table. Oxides of metal elements are generally basic oxides, which either react with h2o to class a basic solution or deliquesce in aqueous acid. In contrast, oxides of nonmetallic elements are acidic oxides, which either react with water to course an acidic solution or are soluble in aqueous base. Oxides of intermediate graphic symbol, chosen amphoteric oxides, are located along a diagonal line between the two extremes. Amphoteric oxides either dissolve in acid to produce water or deliquesce in base of operations to produce a soluble circuitous ion. (Radioactive elements are not classified.)

Figure 17.nine Chromium(III) Hydroxide [Cr(OH)₃ or Cr₂O₃·3H₂O] Is an Example of an Amphoteric Oxide

All three beakers originally contained a suspension of brownish purple Cr(OH)_iii(due south) (eye). When full-bodied acid (six Thou H_iiSo_iv) was added to the beaker on the left, Cr(OH)_iii dissolved to produce violet [Cr(H₂O)_half-dozen]^three+ ions and water. The addition of concentrated base of operations (vi Grand NaOH) to the chalice on the right caused Cr(OH)₃ to deliquesce, producing green [Cr(OH)₄]⁻ions.

Example 8

Aluminum hydroxide, written as either Al(OH)₃ or Al₂O₃·3H_iiO, is amphoteric. Write chemic equations to describe the dissolution of aluminum hydroxide in (a) acid and (b) base.

Given: amphoteric compound

Asked for: dissolution reactions in acid and base

Strategy:

Using Equation 17.28 and Equation 17.29 equally a guide, write the dissolution reactions in acid and base solutions.

Solution:

1. An acrid donates protons to hydroxide to give h2o and the hydrated metallic ion, so aluminum hydroxide, which contains three OH⁻ ions per Al, needs three H⁺ ions:

   Al(OH)₃(due south) + 3H⁺(aq) → Al³⁺(aq) + 3H₂O(l)

   In aqueous solution, Alⁱⁱⁱ⁺ forms the complex ion [Al(H_iiO)_six]³⁺.

2. In basic solution, OH⁻ is added to the compound to produce a soluble and stable poly(hydroxo) complex:

   Al(OH)₃(s) + OH⁻(aq) → [Al(OH)₄]⁻(aq)

Practice

Copper(Two) hydroxide, written equally either Cu(OH)_ii or CuO·H_iiO, is amphoteric. Write chemical equations that describe the dissolution of cupric hydroxide both in an acid and in a base of operations.

Answer:

Cu(OH)₂(s) + 2H⁺(aq) → Cu²⁺(aq) + 2H_iiO(l) Cu(OH)_two(s) + 2OH⁻(aq) → [Cu(OH)_iv]²⁻(aq)

Selective Atmospheric precipitation Using pH

Many dissolved metallic ions can be separated past the selective precipitation of the cations from solution nether specific weather. In this technique, pH is often used to control the concentration of the anion in solution, which controls which cations precipitate.

Note the Pattern

The concentration of anions in solution can often be controlled by adjusting the pH, thereby allowing the selective precipitation of cations.

Suppose, for example, we accept a solution that contains 1.0 mM Zn²⁺ and 1.0 mM Cd^two+ and want to separate the two metals by selective precipitation as the insoluble sulfide salts, ZnS and CdS. The relevant solubility equilibriums tin can be written every bit follows:

Equation 17.30

$$\begin{array}{cc}\hfill \text{ZnS(s)}\rightleftharpoons {\text{Zn}}^{2+}\text{(aq)}+{\text{S}}^{2-}\text{(aq)}& K_{\text{sp}}=1.6\times {\mathrm{x}}^{-24}\end{array}$$

Equation 17.31

$$\begin{array}{cc}\hfill \text{CdS(s)}\rightleftharpoons {\text{Cd}}^{2+}\text{(aq)}+{\text{S}}^{2-}\text{(aq)}& K_{\text{sp}}=\mathrm{viii.0}\times {10}^{-27}\end{array}$$

Because the S^two− ion is quite basic and reacts extensively with water to give HS⁻ and OH⁻, the solubility equilibriums are more accurately written as $\text{MS(southward)}\rightleftharpoons {\text{M}}^{2+}\text{(aq)}+{\text{HS}}^{-}(\text{aq)}+{\text{OH}}^{-}$ rather than $\text{MS(south)}\rightleftharpoons {\text{Chiliad}}^{2+}\text{(aq)}+{\text{S}}^{\mathrm{ii}-}\text{(aq)}\text{.}$ Hither we utilize the simpler grade involving South²⁻, which is justified because we have the reaction of S^two− with h2o into account afterwards in the solution, arriving at the same answer using either equilibrium equation.

The sulfide concentrations needed to cause ZnS and CdS to precipitate are equally follows:

Equation 17.32

$$\begin{array}{cc}\hfill {\mathrm{1000}}_{\text{sp}}& =[{\text{Zn}}^{2+}][{\text{Southward}}^{2-}]\hfill \\ \hfill \mathrm{1.vi}\times {10}^{-24}& =(0.0010\text{ M})[{\text{Due south}}^{2-}]\hfill \\ \hfill \mathrm{1.vi}\times {10}^{-21}\text{ M}& =[{\text{S}}^{2-}]\hfill \end{array}$$

Equation 17.33

$$\begin{array}{cc}\hfill K_{\text{sp}}& =[{\text{Cd}}^{\mathrm{ii}+}][{\text{Due south}}^{\mathrm{two}-}]\hfill \\ \hfill 8.0\times {10}^{-27}& =(0.0010\text{ One thousand})[{\text{S}}^{\mathrm{two}-}]\hfill \\ \hfill 8.0\times {10}^{-24}\text{ M}& =[{\text{S}}^{2-}]\hfill \end{array}$$

Thus sulfide concentrations betwixt i.6 × x⁻²¹ One thousand and 8.0 × ten⁻²⁴ M will precipitate CdS from solution but non ZnS. How do we obtain such low concentrations of sulfide? A saturated aqueous solution of H₂South contains 0.10 M H_twoSouth at 20°C. The pG _a1 for H₂S is 6.97, and pK _a2 corresponding to the formation of [Southⁱⁱ⁻] is 12.90. The equations for these reactions are every bit follows:

Equation 17.34

$$\begin{array}{ccc}\hfill {\text{H}}_2\text{Due south(aq)}\rightleftharpoons {\text{H}}^{+}\text{(aq)}+{\text{HS}}^{-}\text{(aq)}& \text{p}{\mathrm{1000}}_{\text{a1}}=\mathrm{half\; dozen.97}\text{,}& K_{\text{a1}}=1.1\times {\mathrm{x}}^{-7}\\ \hfill {\text{HS}}^{-}\text{(aq)}\rightleftharpoons {\text{H}}^{+}\text{(aq)}+{\text{S}}^{2-}\text{(aq)}& \text{p}{K}_{\text{a}\mathrm{two}}=12.90\text{,}& {\mathrm{One\; thousand}}_{\text{a}\mathrm{ii}}=\mathrm{one.3}\times {10}^{-\mathrm{xiii}}\end{array}$$

Nosotros can evidence that the concentration of S²⁻ is ane.3 × 10⁻¹³ by comparing Yard _a1 and K _a2 and recognizing that the contribution to [H⁺] from the dissociation of HS⁻ is negligible compared with [H⁺] from the dissociation of H_twoSouthward. Thus substituting 0.10 G in the equation for K _a1 for the concentration of H₂Due south, which is substantially constant regardless of the pH, gives the following:

Equation 17.35

$$\begin{array}{cc}\hfill K_{\text{a}1}=1.1\times {10}^{-7}=\frac{[{\text{H}}^{+}][{\text{HS}}^{-}]}{[{\text{H}}_2\text{S}]}& =\frac{{\mathrm{10}}^2}{0.10\text{ Yard}}\hfill \\ \hfill & \mathrm{10}=\mathrm{i.ane}\times {10}^{-\mathrm{iv}}\text{ M}=[{\text{H}}^{+}]=[{\text{HS}}^{-}]\end{array}$$

Substituting this value for [H⁺] and [HS⁻] into the equation for K _a2,

$${\mathrm{Thou}}_{\text{a2}}=1.3\times {10}^{-13}=\frac{[{\text{H}}^{+}][{\text{S}}^{2-}]}{[{\text{HS}}^{-}]}=\frac{(\mathrm{1.ane}\times {10}^{-4}\text{ 1000})\mathrm{ten}}{\mathrm{ane.1}\times {10}^{-4}\text{ 1000}}=x=[{\text{S}}^{\mathrm{two}-}]$$

Although [S^two−] in an H₂S solution is very low (1.three × x^−thirteen Grand), bubbling H₂Southward through the solution until it is saturated would precipitate both metallic ions because the concentration of S²⁻ would and so exist much greater than 1.6 × 10⁻²¹ Chiliad. Thus nosotros must adapt [S²⁻] to stay within the desired range. The most straight manner to do this is to arrange [H⁺] by adding acid to the H_twoSouthward solution (recollect Le Châtelier's principle), thereby driving the equilibrium in Equation 17.34 to the left. The overall equation for the dissociation of H₂S is every bit follows:

Equation 17.36

$${\text{H}}_{\mathrm{ii}}\text{South(aq)}\rightleftharpoons 2{\text{H}}^{+}\text{(aq)}+{\text{Due south}}^{2-}\text{(aq)}$$

Now we can use the equilibrium constant K for the overall reaction, which is the product of Grand _a1 and G _a2, and the concentration of H_twoS in a saturated solution to summate the H⁺ concentration needed to produce [S²⁻] of 1.half dozen × x⁻²¹ M:

Equation 17.37

$$K=M_{\text{a1}}{K}_{\text{a2}}=(\mathrm{1.ane}\times {10}^{-7})(1.3\times {\mathrm{x}}^{-13})=\mathrm{ane.4}\times {\mathrm{x}}^{-20}=\frac{{[{\text{H}}^{+}]}^{\mathrm{ii}}[{\text{Due south}}^{2-}]}{[{\text{H}}_2\text{S}]}$$

Equation 17.38

$$\begin{array}{c}\hfill {[{\text{H}}^{+}]}^2=\frac{K[{\text{H}}_{\mathrm{ii}}\text{S}]}{[{\text{S}}^{2-}]}=\frac{(1.4\times {10}^{-20})(0.10\text{ M})}{\mathrm{ane.half-dozen}\times {10}^{-21}\text{ Thousand}}=0.88\\ \hfill [{\text{H}}^{+}]=0.94\end{array}$$

Thus adding a strong acid such equally HCl to make the solution 0.94 Grand in H⁺ will prevent the more soluble ZnS from precipitating while ensuring that the less soluble CdS volition precipitate when the solution is saturated with H₂S.

Example 9

A solution contains 0.010 M Caⁱⁱ⁺ and 0.010 Thou La³⁺. What concentration of HCl is needed to precipitate La₂(C₂O₄)₃·9H₂O but not Ca(C_iiO₄)·H₂O if the concentration of oxalic acrid is 1.0 Thou? Yard _sp values are ii.32 × 10⁻⁹ for Ca(C₂O₄) and 2.five × 10⁻²⁷ for La₂(C_iiO_four)₃; pThousand _a1 = i.25 and pG _a2 = 3.81 for oxalic acid.

Given: concentrations of cations, K _sp values, and concentration and pK _a values for oxalic acid

Asked for: concentration of HCl needed for selective precipitation of La₂(C₂O₄)_three

Strategy:

A Write each solubility product expression and calculate the oxalate concentration needed for precipitation to occur. Determine the concentration range needed for selective precipitation of La₂(C₂O_four)_three·9H_twoO.

B Add the equations for the outset and 2nd dissociations of oxalic acid to go an overall equation for the dissociation of oxalic acid to oxalate. Substitute the [ox²⁻] needed to precipitate La₂(C₂O₄)_iii·9H₂O into the overall equation for the dissociation of oxalic acrid to calculate the required [H⁺].

Solution:

A Because the salts have different stoichiometries, we cannot directly compare the magnitudes of the solubility products. Instead, nosotros must use the equilibrium constant expression for each solubility production to calculate the concentration of oxalate needed for precipitation to occur. Using ox²⁻ for oxalate, we write the solubility product expression for calcium oxalate as follows:

$$\begin{array}{cc}\hfill G_{\text{sp}}=[{\text{Ca}}^{\mathrm{ii}+}][{\text{ox}}^{2-}]& =(0.010)[{\text{ox}}^{2-}]=2.32\times {\mathrm{x}}^{-\mathrm{nine}}\hfill \\ \hfill [{\text{ox}}^{2-}]& =2.32\times {10}^{-7}\text{ Grand}\hfill \end{array}$$

The expression for lanthanum oxalate is every bit follows:

$$\begin{array}{cc}\hfill K_{\text{sp}}={[{\text{La}}^{\mathrm{iii}+}]}^2{[{\text{ox}}^{\mathrm{two}-}]}^3& ={(0.010)}^2{[{\text{ox}}^{2-}]}^3=2.5\times {10}^{-27}\hfill \\ \hfill [{\text{ox}}^{2-}]& =2.9\times {10}^{-\mathrm{eight}}\text{ M}\hfill \end{array}$$

Thus lanthanum oxalate is less soluble and will selectively precipitate when the oxalate concentration is betwixt ii.9 × 10⁻⁸ Chiliad and 2.32 × 10⁻⁷ Yard.

B To prevent Ca²⁺ from precipitating as calcium oxalate, we must add plenty H⁺ to give a maximum oxalate concentration of 2.32 × 10⁻⁷ One thousand. We can calculate the required [H⁺] by using the overall equation for the dissociation of oxalic acid to oxalate:

$${\text{HO}}_2{\text{CCO}}_2\text{H(aq)}\rightleftharpoons 2{\text{H}}^{+}\text{(aq)}+{\text{C}}_2{\text{O}}_{\mathrm{iv}}{}^{2-}\text{(aq)}$$ $$K=K_{\text{a1}}{K}_{\text{a2}}=({\mathrm{x}}^{-1.25})({10}^{-3.81})={10}^{-5.06}=\mathrm{eight.7}\times {10}^{-\mathrm{half-dozen}}$$

Substituting the desired oxalate concentration into the equilibrium constant expression,

$$\begin{array}{ccc}\hfill 8.7\times {\mathrm{x}}^{-6}& =\frac{{[{\text{H}}^{+}]}^{\mathrm{ii}}[{\text{ox}}^{2-}]}{[{\text{HO}}_{\mathrm{two}}{\text{CCO}}_2\text{H}]}\hfill & =\frac{{[{\text{H}}^{+}]}^{\mathrm{two}}(2.32\times {10}^{-7})}{1.0}\hfill \\ \hfill & [{\text{H}}^{+}]& =6.1\text{ G}\hfill \end{array}$$

Thus calculation enough HCl to requite [H⁺] = six.1 M will cause simply La_two(C₂O₄)_three·9H_twoO to precipitate from the solution.

Exercise

A solution contains 0.015 Grand Iron²⁺ and 0.015 M Lead²⁺. What concentration of acrid is needed to ensure that Pb^two+ precipitates as PbS in a saturated solution of H₂S, but Feⁱⁱ⁺ does not precipitate as FeS? K _sp values are half-dozen.3 × 10⁻¹⁸ for FeS and 8.0 × 10⁻²⁸ for PbS.

Answer: 0.018 M H⁺

Summary

The anion in many sparingly soluble salts is the conjugate base of a weak acid. At low pH, protonation of the anion tin dramatically increment the solubility of the salt. Oxides can be classified as acidic oxides or basic oxides. Acidic oxides either react with water to give an acidic solution or dissolve in stiff base of operations; near acidic oxides are nonmetal oxides or oxides of metals in high oxidation states. Bones oxides either react with water to give a bones solution or dissolve in strong acid; well-nigh basic oxides are oxides of metallic elements. Oxides or hydroxides that are soluble in both acidic and basic solutions are chosen amphoteric oxides. Well-nigh elements whose oxides exhibit amphoteric beliefs are located along the diagonal line separating metals and nonmetals in the periodic table. In solutions that contain mixtures of dissolved metal ions, the pH can be used to control the anion concentration needed to selectively precipitate the desired cation.

Central Takeaway

• The anion in sparingly soluble salts is ofttimes the conjugate base of a weak acid that may become protonated in solution, so the solubility of simple oxides and sulfides, both strong bases, ofttimes depends on pH.

Conceptual Bug

1. Which of the following will bear witness the greatest increase in solubility if 1 M HNO₃ is used instead of distilled water? Explain your reasoning.

   1. CuCl_ii
   2. K[Pb(OH)₃]
   3. Ba(CH₃CO₂)_ii
   4. CaCO₃

2. Of the compounds Sn(CH₃CO₂)₂ and SnS, one is soluble in dilute HCl and the other is soluble only in hot, concentrated HCl. Which is which? Provide a reasonable caption.

3. Where in the periodic table do you await to detect elements that grade basic oxides? Where practice you wait to notice elements that course acidic oxides?

4. Because h2o can autoionize, it reacts with oxides either as a base (every bit OH⁻) or equally an acid (as H_threeO⁺). Do you expect oxides of elements in high oxidation states to be more acidic (reacting with OH⁻) or more bones (reacting with H₃O⁺) than the corresponding oxides in depression oxidation states? Why?

5. Given solid samples of CrO, Cr_iiO_three, and CrO₃, which would you wait to be the virtually acidic (reacts nigh readily with OH⁻)? Which would be the most basic (reacts most readily with H_iiiO⁺)? Why?

6. Which of these elements—Exist, B, Al, N, Se, In, Tl, Atomic number 82—exercise you look to form an amphoteric oxide? Why?

Numerical Problems

1. A 1.0 L solution contains 1.98 Yard Al(NO₃)_three. What are [OH⁻] and [H⁺]? What pH is required to precipitate the cation as Al(OH)₃? K _sp = ane.3 × 10⁻³³ and M _a = 1.05 × 10⁻⁵ for the hydrated Al³⁺ ion.

2. A 1.0 L solution contains 2.03 One thousand CoCl₂. What is [H⁺]? What pH is required to precipitate the cation every bit Co(OH)_two? K _sp = 5.92 × 10^−fifteen and M _a = 1.26 × 10^−nine for the hydrated Co^two+ ion.

3. Given 100 mL of a solution that contains 0.80 mM Ag⁺ and 0.lxxx mM Cu⁺, can the 2 metals exist separated past selective precipitation every bit the insoluble bromide salts by adding 10 mL of an 8.0 mM solution of KBr? Thou _sp values are half-dozen.27 × 10⁻⁹ for CuBr and 5.35 × x⁻¹³ for AgBr. What maximum [Br⁻] will split up the ions?

4. Given 100 mL of a solution that is ane.v mM in Tl⁺, Zn^two+, and Ni²⁺, which ions can exist separated from solution past adding five.0 mL of a 12.0 mM solution of Na₂C₂O₄?

   Precipitate	K sp
   Tl2C2Ofour	2 × 10−four
   ZnC2Ofour·2H2O	one.38 × 10−9
   NiCtwoO4	4 × x−10

   How many milliliters of 12.0 mM Na_iiC₂O_iv should be added to carve up Tl⁺ and Zn²⁺ from Ni²⁺?

Answers

1. [H⁺] = 4.56 × x⁻ⁱⁱⁱ; [OH⁻] = 2.19 × 10⁻¹²; pH = 2.94

3. No; both metal ions volition precipitate; AgBr volition precipitate as Br⁻ is added, and CuBr will begin to precipitate at [Br⁻] = eight.6 × ten⁻⁶ M.

stittzookinat.blogspot.com

Source: https://saylordotorg.github.io/text_general-chemistry-principles-patterns-and-applications-v1.0/s21-04-solubility-and-ph.html

Share this post